以下、本文になります
解析学研究室
教員
竹井 義次(教授)Yoshitsugu TAKEI
DB| 研究分野 | 解析学・微分方程式 |
|---|---|
| 研究室 | HS-310 |
| TEL | 0774-65-6653 |
| FAX | |
| ytakei@mail.doshisha.ac.jp |
プロフィール(略歴)
1961年京都市生まれ。1984年京都大学理学部卒業。1990年京都大学理学博士。 京都大学理学部数学教室助手、京都大学数理解析研究所助教授/准教授を経て、 2017年より現職。この間、バークレー数理科学研究所ポスドク、ニース大学 客員教授、ストラスブール大学客員教授、さらに日本学術振興会の特定国 派遣研究者事業や二国間科学協力事業でサクレー原子核研究センター、 サウザンプトン大学、シドニー大学、メリーランド大学に滞在等、外国の大学や 研究機関でも数多く研究を行ってきました。趣味は旅行やドライブ。特に 、 バークレーに滞在したときに車で北米大陸を横断したことは良い思い出です。
専門分野
- 微分方程式
- 漸近解析
- 超局所解析
- 複素解析
- 特殊函数論
代表的な仕事
複素領域の常微分方程式論における一つの中心課題は、解の大域挙動の解析です。例えば、特異点がすべて確定特異点と呼ばれるおとなしい型の特異点から成るフックス型方程式の場合、独立変数を大域的に動かした時の解の変化を記述するモノドロミー群が解の大域挙動を完全に決定します。 しかし、rigidと呼ばれる 一部の方程式を除いて、一般にモノドロミー群を求めることは非常に難しい問題です。
私は、河合隆裕氏や青木貴史氏と共同で、小さなパラメータを含む1次元シュレディンガー方程式の形をした2階のフックス型線型常微分方程式に対して、 WKB解と呼ばれる漸近解にボレル総和法を適用することにより、そのモノドロミー群をWKB解のボレル和を用いて具体的に計算する処方箋を与えることに成功しました。 この方法は、漸近解析的な性格をもつ接続公式と複素解析に固有の留数解析を組み合わせるもので、留数解析による積分計算と同様に非常に明示的にモノドロミー群を計算できる点が気に入っています。
研究テーマ
(1)線型常微分方程式の完全WKB解析
最も簡単で基本的な2階線型常微分方程式 $(\epsilon^2 d^2/dx^2 - 1) u = 0$(ただし $\epsilon$ は小さなパラメータ)の解は、$u =
\exp (\pm x/\epsilon)$ と指数関数を用いて表されます。ところが、係数を関数 $Q(x)$ で置き換えた $(\epsilon^2 d^2/dx^2 - Q(x)) u = 0$
を考えると、微分方程式の解を具体的に書き下すことは急に難しくなります。
この場合でも、WKB解と呼ばれる $u = \exp ((u_0(x)+u_1(x)\epsilon+\cdots)/\epsilon)$ という形の解を構成することは可能ですが、残念ながらこの解は収束しません。このWKB解に、フーリエ・ラプラス解析と密接に関係する「ボレル総和法」という一種の"手品"を用いて数学的な意味づけを行うのが完全WKB解析です。ボレル総和法を用いれば、解の大域的性質を(独立変数を複素数に拡張した上で)調べることが可能になります。
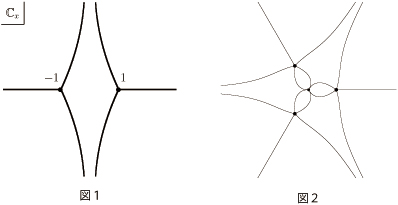
例えば $Q(x)=x^2-1$ の場合にWKB解にボレル総和法を適用すると、(ストークス図形と呼ばれる)図1に現われる複素平面内の各領域毎に異なる解が得られます。こうしたストークス図形の幾何学的性質を援用しながら、WKB解を用いてシュレディンガー方程式の固有値や複素領域における線型常微分方程式の解の大域的性質を研究することが私の第一の研究テーマです。
この場合でも、WKB解と呼ばれる $u = \exp ((u_0(x)+u_1(x)\epsilon+\cdots)/\epsilon)$ という形の解を構成することは可能ですが、残念ながらこの解は収束しません。このWKB解に、フーリエ・ラプラス解析と密接に関係する「ボレル総和法」という一種の"手品"を用いて数学的な意味づけを行うのが完全WKB解析です。ボレル総和法を用いれば、解の大域的性質を(独立変数を複素数に拡張した上で)調べることが可能になります。
例えば $Q(x)=x^2-1$ の場合にWKB解にボレル総和法を適用すると、(ストークス図形と呼ばれる)図1に現われる複素平面内の各領域毎に異なる解が得られます。こうしたストークス図形の幾何学的性質を援用しながら、WKB解を用いてシュレディンガー方程式の固有値や複素領域における線型常微分方程式の解の大域的性質を研究することが私の第一の研究テーマです。

(2)パンルヴェ方程式の漸近解析
20世紀初頭にパンルヴェによって発見されたパンルヴェ方程式は、KdV方程式等のソリトン型の偏微分方程式(いわゆる可積分系)やモノドロミー保存変形とも関係する重要な常微分方程式であり、最近は代数や幾何、物理といった解析以外の分野の専門家も含めて多方面から研究されています。パンルヴェ方程式は2階の非線型方程式ですが、上で述べた完全WKB解析は、このパンルヴェ方程式の解析にも威力を発揮します。例えば、II型のパンルヴェ方程式 $\epsilon^2 d^2 u/dx^2 = 2u^3 + xu +1$ の場合のストークス図形を表したのが 図2です。図1と比べるとかなり複雑な図になりますが、やはりこの場合も、ボレル総和法によって図2の各領域毎にII型パンルヴェ方程式の解が得られます。 パンルヴェ方程式や、さらに最近はパンルヴェ型の差分方程式の解の漸近的性質を、完全WKB解析の立場から研究しています。