以下、本文になります
数理工学研究室
教員
多久和 英樹(教授)Hideki TAKUWA
DB| 研究分野 | 偏微分方程式論と数学的逆問題 |
|---|---|
| 研究室 | YM-221 |
| TEL | 0774-65-6431 |
| FAX | |
| htakuwa@mail.doshisha.ac.jp |
伊縫 寛治(助教)Kanji INUI
DB| 研究分野 | エルゴード理論とフラクタルの研究 |
|---|---|
| 研究室 | YM-422 |
| TEL | 0774-65-6492 |
| FAX | |
| kinui@mail.doshisha.ac.jp |
研究内容
物理現象や工学の問題は微分方程式により記述される。当研究室では、流体流れや熱伝達および熱伝導の問題を記述する偏微分方程式の解の性質を数学解析および数値シミュレーションによって調べ、物理現象および工学的問題を解決するための研究を行っている。水島二郎教授は、 流体中に発生する運動をいろいろな角度から眺め,解析し,研究を行っている。 特に、流れの不安定性と乱流への遷移を中心に研究を行っている。流れが不安定になると流れのパターンが突然変化する。 また、流れの不安定性の結果、流れが時間的に振動流となり、 物体の振動を誘起することがある。 このような流れの安定性理論の応用として、流れのパターンを人為的に作り出すことや流れの中に発生する振動を制御することが可能である。逆に流れの中に意図的に振動を発生することによって機械を制御することも可能となる。多久和英樹教授は、自然現象の数学的定式化としての微分方程式とその最適な数値解析に主眼をおく研究を行っている。1.理工学に現れる偏微分方程式に対する逆問題
理工学分野において、偏微分方程式で記述される現象は多い。その中でも、逆問題と呼ばれる分野は、構造物の亀裂の探査、地下資源の探査、残留応力の非破壊検査、材料特性の検査など各種の応用例に対する基礎理論を成す。偏微分方程式に対する逆問題を解析するためには、現象の数学的背景、特に偏微分方程式論の解の構造等、通常の初期値問題や境界値問題に現れない深い構造の理解が必要である。この点を踏まえ、数学的背景から実際の応用までを考察の対象としている。2.同軸回転2円板間流れの不安定性と遷移
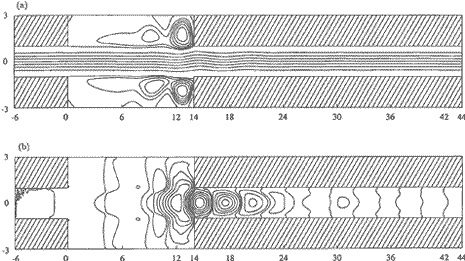
コンピュータのハードディスク内部流のモデルである同軸回転2円板間の流れについて、実験と数値シミュレーションおよび解析により調べる。3.急拡大部と急縮小部をもつ管路流れの数値シミュレーション
急拡大部と急縮小管をもつ管路流れの数値シミュレーションを行い、安定性の理論から得られた結果と比較する。
4.円管ポワズイユ流の安定性
現在円管ポアズイユ流は線形理論では安定であることがわかっている。円管ポアズイユ流の安定性を数値シミュレーション・非線形安定性理論等を用いて調べる
5.球、円柱および円柱列を過ぎる流れの不安定性と遷移
球、円柱および円柱列を過ぎる流れの定常解を求めその線形安定性を調べることにより、解の分岐の構造を調べる。

6.2円柱を過ぎる流れの遷移
流れ方向、および流れと垂直に並んだ2つの円柱の流れの振動流や偏向流への遷移について数値解析、実験の両面から調べる。

7.立軸ポンプにおける吸込み渦の発生
軸流ポンプでは、一般にラッパ状の吸込口(ベルマウス形状)を使用するが、この形状を小型化し、かつ最適化することをめざす。

8.バックステップ流れの渦構造
急拡大部をもつ管路流れの数値シミュレーションを行い、安定性の理論から得られた結果と比較する。9.バスタブ渦の発生機構
小さな流出口をもつ容器から流体が流出するときに、流出口付近にバスタブ渦が発生する。
このバスタブ渦の発生とその構造を実験、数値解析の双方から調べる。
このバスタブ渦の発生とその構造を実験、数値解析の双方から調べる。

10.エクラノプラン
エクラノプランは地面効果により大きな揚力を得ることができる。地面、水面を問わずこの効果が得られるために、将来的には大陸間の輸送手段としても期待されている。
エクラノプランのモデルを作り実験を行う。
11.風力発電装置の基本的研究
ヨーロッパやアメリカでは風力発電が盛んに研究され実用化されているが日本ではまだ一般的ではない。事業用の大規模発電ではなく家庭用の小さい風力発電装置の開発をめざす。
12.風に向かって進む風力自動車の模型の開発
風に向かって進む自動車を作ることができるかどうか。これは実用をめざすものではなく知的なおもちゃとして取り組む。
13.流体を用いたおもちゃの開発
流体の特性、特に流体中の振動現象を利用したおもちゃを開発する。また、流体中での音の発生を利用した、楽器を開発する。